In here are the list of things I did for a particular hour or day. Also included here are the screenshots of games I played, or videos I watched or listened to, or just random things I stumbled upon. I'll occasionally write down what I'm thinking, or things I'm planning to do.

• [ 2024-02-28 ]
• 19:15 [link] [context] #sn

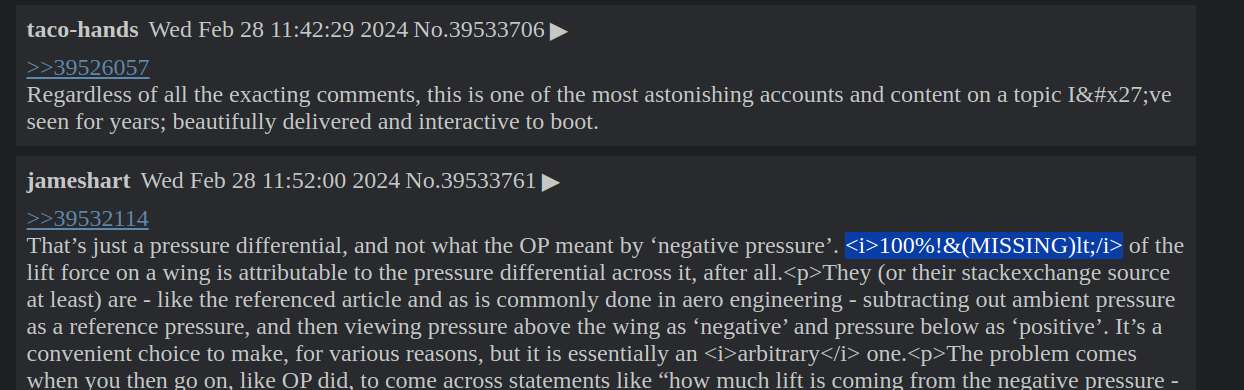
  Urgh, I can't believe I spent almost an hour finding out what's causing the <i>100%!&(MISSING)lt;/i> bug. I though encoding/json was escaping %, but no. I thought gopher-lua was doing some weird string escaping, no again. I thought gopher-luar was doing some weird string escaping, nope.

  Then I thought of printing the text right before writing the response back. Curl was showing the broken text, but the printed text shows the text properly.

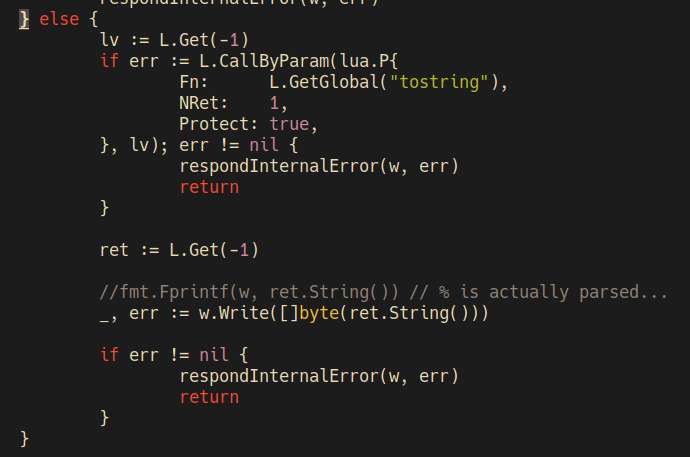
  Aha, by process of elimination, the source of bug was the code writing the response back:

  fmt.Fprintf(w, ret.String())

  Well of course, fmt uses % to format string, no shit. I feel so retarded now in hindsight.

  I tried googling for %!&(MISSING) but it shows me an FBI kidnappings and missing person list, lots of kids too. Uh-oh. Damn, look at all the unresolved cases, some dating back all the way to 2010.

  I'm reminded that the world is a scary place, you'll never know what sick fuck is lurking around the corner.

• 16:48 [link] [context] #sn

  Still mostly worked on making the UI look like *chan forum. I found a bug where some tags wouldn't close and end up like `<i>100%!&(MISSING)lt;/i>`. It doesn't happen with direct curl to HN API, so the problem is most likely my escaping function, or the json parser.

• 12:14 [link] [context] #math

  Did some "studying" on my rocketbook with calculus notations. I tried writing it in a lua notation so it would be clear what scope each variable is, and are the dependent variables.

  One thing I did realize is that Δx is not locally scoped inside the derivative, and that ε isn't really an independent variable as the book suggests.

  So once I again, I will try to start from scratch, and write all the functions and equations:

  let ∆x be any infinitesimal
  let dx = ∆x
  let f: func(x: *R)
  
  let derivative = f => x => st{ [f(x + ∆x) - f(x)]∆x~ }
  let differential = f => x => derivative(f)(x) * dx
  
  let x be any infinitesimal
  let y = f(x)
  let slope = derivative(f)(x)
  let dy = differential(f)(x)

  The book sometimes defines derivatives in terms of differentials, and differentials in terms of derivatives. I think it depends on which unknown variables are, or which side makes the computation easier. I don't know, I understand it in principle, but I'm not sure how to apply it in practice yet.

  I found an HN post linking to a page of cool stuffs that applies math with programming. In particular, there's Differential equations and calculus from scratch which is highly relevant to what I'm doing.

• 

  🕚 11:29

  

  🕚 11:10

  

  🕚 11:10

  

  🕙 10:25

  

  🕙 10:25

  

  🕙 10:25

  

  🕙 10:19

  

  🕙 10:18

  

  🕙 10:17

  

  🕙 10:16

  

  🕙 10:16

  

  🕙 10:15

  

  🕗 08:48

  

  🕗 08:47

  

  🕗 08:44

  

  🕔 05:19

  

  🕓 04:14

site last updated on 2024-10-16 | created with moontpl